Series circuits

07/05/2026

The online series circuit simulations on this page let you interactively understand how current, voltage, and equivalent resistance behave in a simple circuit. Through virtual setups with a power source, switch, light bulbs, resistors, ammeters, and voltmeters, you can see the relationship between circuit current, resistance values, and voltage drops at different points.

This Thematic Unit is part of our Circuits collection

Continuity

Presence of a complete path for current flow; if one component fails in series, continuity is lost throughout the circuit.

Equivalent Resistance

A single resistance that could replace all those in the circuit producing the same effect; in series, it is the sum of all of them.

Series Circuit

Configuration where components are connected one after another, so that the same current flows through all of them.

Voltage (Tension)

Electric potential difference between two points in a circuit that drives the movement of charges, measured in Volts (V).

Voltage Divider

Configuration of resistors in series that distributes the total source voltage proportionally to each resistor.

Voltage Drop

Decrease in electric potential when passing through a resistive component due to the energy consumption of the charges.

What are series circuits?

Series circuits are characterized by their components being connected one after another, forming a single path for current to flow. In this kind of setup, the current passing through each element is the same, while the total voltage from the source is distributed among the different components in proportion to their values. The equivalent resistance is found by directly adding up all the connected resistances. Series circuits are a basic and simple configuration that lays the foundation for analyzing more complex configurations.

Formula for equivalent resistance

When several resistors are connected in series, their combined effect on the circuit can be expressed as a single equivalent resistance. This equivalent resistance is obtained by simply adding together the values of all the connected resistors:

R_eq= R₁ + R₂ + R₃ +…+ R_n

The current that flows through each resistor is the same, and the total voltage applied to the circuit is divided among them. In this way, the equivalent resistance represents the total opposition to the flow of current in that single path formed by the series resistors.

Practical example

Let’s suppose we have three resistors connected in series with values of 10 Ω, 20 Ω, and 30 Ω. The equivalent resistance of the circuit is found by directly adding their values:

R_eq = 10 + 20 + 30 = 60 Ω

This means that, from the perspective of the power source, the set of resistors behaves like a single 60 Ω resistor. The current flowing through each resistor is the same, while the total applied voltage is shared among them in proportion to their resistance value. For example, if the source provides 12 V, the voltage drop will be 2 V across the 10 Ω resistor, 4 V across the 20 Ω resistor, and 6 V across the 30 Ω resistor, which adds up to the total 12 V.

Continuity

Presence of a complete path for current flow; if one component fails in series, continuity is lost throughout the circuit.

Equivalent Resistance

A single resistance that could replace all those in the circuit producing the same effect; in series, it is the sum of all of them.

Series Circuit

Configuration where components are connected one after another, so that the same current flows through all of them.

Voltage (Tension)

Electric potential difference between two points in a circuit that drives the movement of charges, measured in Volts (V).

Voltage Divider

Configuration of resistors in series that distributes the total source voltage proportionally to each resistor.

Voltage Drop

Decrease in electric potential when passing through a resistive component due to the energy consumption of the charges.

Explore the exciting STEM world with our free, online, simulations and accompanying companion courses! With them you’ll be able to experience and learn hands-on. Take this opportunity to immerse yourself in virtual experiences while advancing your education – awaken your scientific curiosity and discover all that the STEM world has to offer!

Series circuit simulations

Constant current

In this simulation, a circuit is built with a power source, a switch, a light bulb, and several resistors connected in series. Several ammeters are placed at different points in the circuit to check that all register the same current value. Notice how, no matter how many resistors are added or what their values are, the current that flows is always the same throughout the path. Change the values of the resistors and the battery voltage to verify that this property always holds in series connections.

Equivalent resistance in a series circuit

In this simulation, a circuit is built with a power source, a switch, a light bulb, and several resistors connected in series. An ammeter is placed anywhere in the circuit and a voltmeter is placed across the resistors. Calculate the equivalent resistance by measuring the total voltage and applying Ohm’s Law (Req = V/I). Check that the result matches the sum of the individual resistances. Modify the values of the resistors and the battery voltage to see that this rule always applies.

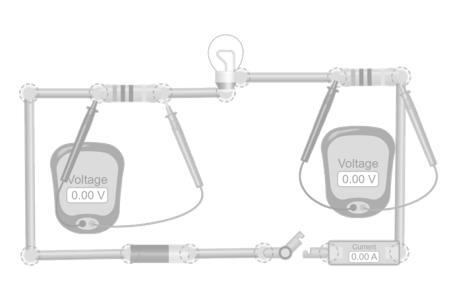
Voltage distribution in series circuits

In this simulation, a circuit is built with a power source, a switch, a light bulb, and several resistors connected in series. An ammeter is placed in series with the power source to measure the current. Additionally, voltmeters are used across each resistor and across the complete set. Observe how the total battery voltage is divided among the resistors in proportion to their values, and how the sum of the partial voltage drops matches the total applied voltage. Change the values of the resistors and the battery voltage to verify that this rule is always fulfilled.

Giants of science

“If I have seen further, it is by standing on the shoulders of giants”

Isaac Newton

André-Marie Ampère

1775

–

1836

André-Marie Ampère formulated the theory of electromagnetism, establishing the mathematical foundations linking electricity and magnetism

“Science is the explanation of the complex by the simple”

Michael Faraday

1791

–

1867

Michael Faraday discovered electromagnetic induction, conducted pioneering experiments in optics (Faraday effect), and established fundamental principles of electrochemistry.

“Nothing is too wonderful to be true”

Become a giant

Your path to becoming a giant of knowledge begins with these top free courses

Free mode

Principles of Modeling, Simulations, and Control for Electric Energy Systems

Free mode

Principles of Electric Circuits | 电路原理

Free mode

Electrotechnique I

Free mode

Electromagnetic Compatibility Essentials

Professional development for Educators

Your path to becoming a giant of knowledge begins with these top free courses

Free mode

Teach teens computing: How computers work

Free mode

Teaching with Physical Computing: Introduction to Project-Based Learning

Free mode

Introduction to Data Wise: A Collaborative Process to Improve Learning & Teaching

Free mode

Teach teens computing: Databases and SQL

Giants of science

“If I have seen further, it is by standing on the shoulders of giants”

Isaac Newton

James Clerk Maxwell

1831

–

1879

James Clerk Maxwell formulated Maxwell’s equations, unifying electricity and magnetism and predicting electromagnetic waves

“Thoroughly conscious ignorance is the prelude to every real advance in science”

Michael Faraday

1791

–

1867

Michael Faraday discovered electromagnetic induction, conducted pioneering experiments in optics (Faraday effect), and established fundamental principles of electrochemistry.

“Nothing is too wonderful to be true”

Become a giant

Your path to becoming a giant of knowledge begins with these top free courses

Free mode

Principles of Modeling, Simulations, and Control for Electric Energy Systems

Free mode

Principles of Electric Circuits | 电路原理

Free mode

Electrotechnique I

Free mode

Electromagnetic Compatibility Essentials

Professional development for Educators

Your path to becoming a giant of knowledge begins with these top free courses

Free mode

Teaching and Learning in the Era of AI

Free mode

Advancing Learning Through Evidence-Based STEM Teaching

Free mode

Learning How to Learn: Unlocking a Growth Mindset with AI

Free mode

Teaching with Physical Computing: Assessment of Project-Based Learning

Test your knowledge

What is a series circuit?

A series circuit is a type of electrical circuit in which components such as resistors, bulbs, or devices are connected one after another in a single path, so that the same electric current flows through all of them. This arrangement means that any interruption in one component stops the flow of current throughout the entire circuit, and it allows for a straightforward analysis of how electrical energy is distributed, since the voltage is shared among the different elements while the current remains constant along the whole path.

How do current and voltage behave in a series circuit?

In a series circuit, the electric current is the same through all components because there is only one possible path for it to flow, while the total voltage supplied by the source is divided among the different elements depending on their characteristics, especially their resistance. This means that each component receives only part of the total energy, and understanding how that energy is distributed along the circuit makes it possible to predict its behavior and calculate electrical quantities accurately.

Why do all the bulbs go out if one stops working in a series circuit?

This happens because in a series circuit all components are connected in a single continuous path, so if one of them fails or the connection is broken, the circuit becomes open and the current stops flowing completely. It is similar to breaking a chain at one link, since there is no alternative path for the current to follow, which means that all devices stop receiving energy and turn off, making this type of circuit less suitable when independent operation of components is needed.

Why do bulbs get dimmer when several are connected in series?

When several bulbs are connected in series, the total voltage provided by the source is shared between them, so each bulb receives only a portion of the available energy, which results in a lower light intensity compared to a single bulb connected alone. In addition, as more components are added in series, the total resistance of the circuit increases, which can reduce the current if the power source is limited, further contributing to the decrease in brightness.

Are series circuits used in real life or are they just theoretical?

Series circuits are used in real life, although they have important limitations because all components depend on each other, which can make them impractical in many situations. However, they are still used in simple devices, in some older lighting systems, and especially in educational contexts because they help illustrate basic electrical principles clearly, and they can also be useful in situations where all components are intended to operate together or where a simple and cost-effective design is required.