Las simulaciones online de lentes ópticas delgadas de esta página te van a ayudar a entender mejor cómo es la óptica geométrica de las lentes delgadas. Esta página sirve como introducción a las páginas de lentes convexas o convergentes y lentes cóncavas o divergentes
Qué son las lentes ópticas delgadas
Las lentes ópticas son dispositivos que se utilizan para controlar y enfocar la luz. Están compuestas por materiales transparentes, como el vidrio o el plástico, y tienen una forma curva que permite que la luz se refracte y se enfoque en un punto específico.
Se entiende por lente delgada aquella que tiene un grosor muy pequeño en comparación con su radio de curvatura. Esta simplificación permite usar aproximaciones matemáticas más simples para describir cómo la luz se comporta al atravesarla.
Óptica geométrica
La óptica geométrica es la parte de la óptica que trata, a partir de representaciones geométricas, de los cambios de dirección que experimentan los rayos luminosos en los distintos fenómenos de reflexión y refracción.
La óptica geométrica parte de los siguientes supuestos:
– La luz se propaga rectilíneamente
– Los rayos luminosos son reversibles. El camino seguido por un rayo es independiente de que se produzca en un determinado sentido o en su contrario.
– Se cumplen las leyes de la reflexión y de la refracción.
Tipos de lentes ópticas delgadas
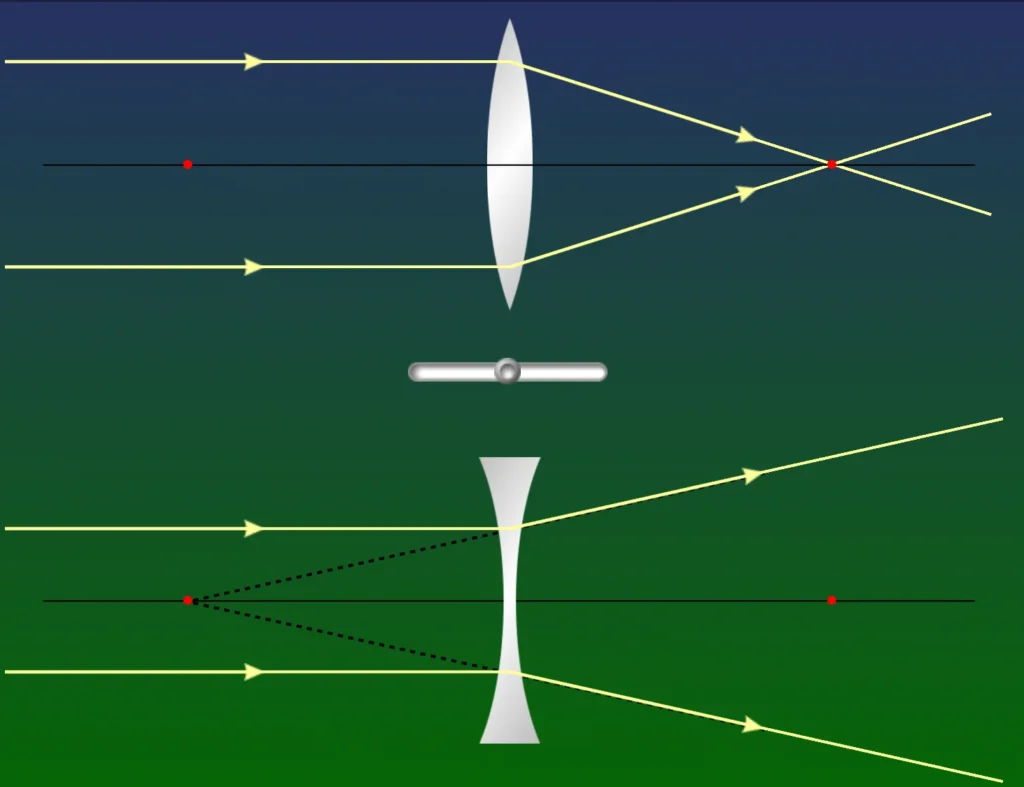
Las lentes delgadas pueden ser de dos tipos principales:
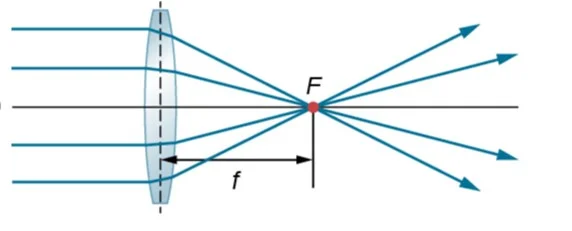
Lentes convexas o convergentes. Estas lentes son más gruesas en el centro que en los bordes y hacen que los rayos de luz que pasan a través de ellas converjan en un punto, conocido como foco. Aquí tienes información más detallada sobre este tipo de lentes
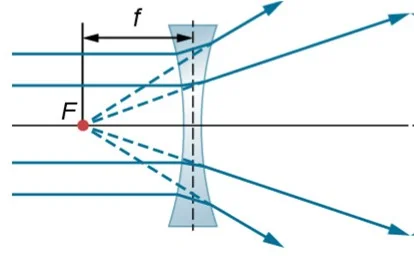
Lentes cóncavas o divergentes. Estas lentes son más delgadas en el centro que en los bordes y hacen que los rayos de luz que pasan a través de ellas diverjan como si vinieran de un punto focal situado delante de la lente. Aquí tienes información más detallada sobre este tipo de lentes
Parámetros de las lentes ópticas delgadas
Los parámetros principales que caracterizan a una lente óptica son:
Foco (F). El foco es el punto donde los rayos paralelos al eje principal convergen en una lente convergente, o divergen en una lente divergente).
Centro óptico (O). el centro óptico es el punto de la lente a través del cual los rayos de luz pasan sin desviarse.
Distancia focal (f). La distancia focal es la distancia entre el centro óptico de la lente y el foco.
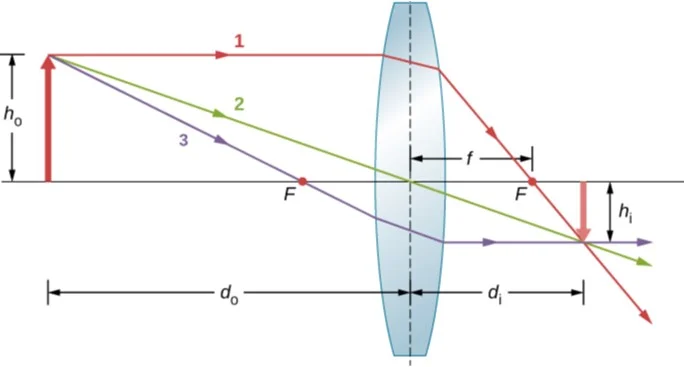
Ecuaciones de las lentes ópticas delgadas
La ecuación principal de las lentes delgadas relaciona la distancia focal de la lente con la distancia del objeto y la distancia de la imagen y se expresa como:
1/f = 1/d0 + 1/di
Donde
f distancia focal
do distancia del objeto
di distancia de la imagen
Por convención, se considera que las distancias de los objetos y las imágenes son positivas si si están en el lado opuesto al del origen de la luz y negativas si están ene l mismo lado.
Un concepto crucial de una lente es la magnificación, es decir la medida de cuánto se agranda o se reduce la imagen de un objeto al pasar a través de una lente. La magnificación de una lente delgada se define como el cociente entre la altura de la imagen y la altura del objeto, y está directamente relacionado con las distancias del objeto y la imagen:
M = hi/h0 = -di/d0
Donde
M magnificación
ho altura del objeto
hi altura de la imagen
do distancia del objeto
di distancia de la imagen
Los valores de M hay que interpretarlo de la siguiente forma:
M positiva La imagen es virtual y derecha
M negativa La imagen es real e invertida
Valor absoluto M >1 La imagen es más grande que el objeto
Valor absoluto M < 1 La imagen es más pequeña que el objeto
Ejemplo. Supongamos un objeto de altura ho que forma una imagen de altura hi. Si la distancia del objeto d0 es de 10 cm y la distancia de la imagen di es de -20cm (imagen virtual), aplicando la ecuación de la magnificación se obtiene que:
M = -di/d0 = – (-20)/10 =2
Es decir la imagen virtual es derecha (igual orientación que el objeto) y del doble de tamaño.
La magnificación de una lente delgada es un concepto crucial en muchos dispositivos ópticos (microscopios, telescopios, cámaras, etc.) y su comprensión es fundamental para el diseño y uso de dispositivos ópticos.
Parámetros de diseño de una lente óptica delgada
¿Cómo se puede diseñar una lente para que actúe como deseamos? Hay tres parámetros de diseño básicos sobre los que se puede actuar: el material, el grosor y la curvatura.
El material de la lente determina características básicas como son su transparencia o su índice de refracción.
El espesor de una lente se refiere a la distancia entre sus dos superficies, medida a lo largo de la línea central de la lente y puede ser uniforme o puede variar a lo largo de la lente, lo que se conoce como una lente de grosor variable.
La curvatura de una lente se refiere a la forma de sus superficies, que pueden ser cóncavas (curvatura hacia adentro) o convexas (curvatura hacia afuera), lo cual da lugar a las lentes divergentes y convergentes respectivamente. La curvatura de una lente se mide en dioptrías (D) y está relacionada con la capacidad de la lente para refractar la luz. Una lente más curva tendrá una mayor capacidad de refracción que una lente menos curva.
El material, el espesor y la curvatura de una lente óptica delgada son tres de las características más importantes que determinan su comportamiento óptico. Estos tres parámetros van a determinar la posición del foco y la distancia focal y, en definitiva, el comportamiento de la lente.
Observa en nuestras simulaciones de lentes ópticas delgadas como al modificar estos parámetros de una lente se obtienen resultados distintos. Observa que imágenes producen distintos tipos de lentes, qué ocurre al modificar el material (índice de refracción), el espesor y la curvatura de una lente.
Si deseas ampliar algo más tus conocimientos sobre lentes ópticas visita nuestras páginas de lentes convexas y lentes cóncavas.
Aplicaciones de las lentes ópticas delgadas
Las lentes ópticas tienen una amplísima gama de aplicaciones en diversos campos. Algunos de los ejemplos que se pueden citar son gafas, lentes de contacto y lentes intraoculares; cámaras fotográficas y videocámaras; microscopios, telescopios, periscopios y binoculares; proyectores, pantallas y monitores; espectrómetros e interferómetros; lámparas, faros y luces de automóviles; endoscopios y láseres médicos; sistemas de visión artificial, lectores de códigos de barras; gafas de realidad aumentada y cascos de realidad virtual; fibra óptica y equipos de medición óptica.
Simulaciones de lentes ópticas delgadas
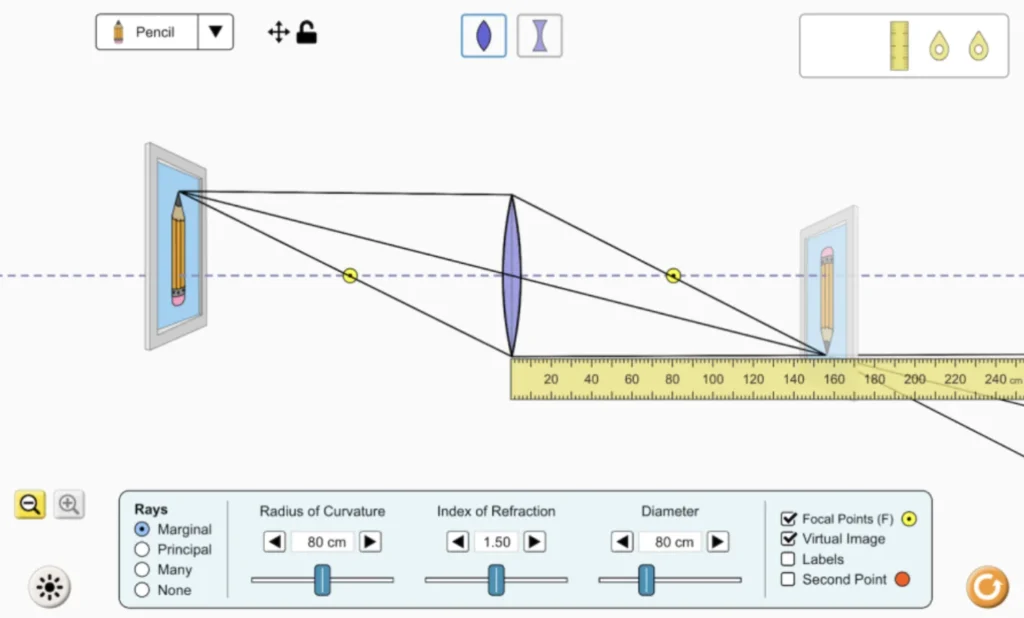
Laboratorio virtual de lentes delgadas
En esta simulación de lentes delgadas se puede estudiar qué ocurre en la imagen formada por una lente al cambiar la distancia focal y la altura y posición del objeto.
Cuando estés listo para empezar, pulsa el botón «Begin».
Optica geométrica I
En esta primera simulación de la óptica geométrica de las lentes delgadas, se explica cómo se forma una imagen con una lente convergente o un espejo plano. Determina cómo el cambio de los parámetros de una lente afecta el lugar donde se forma la imagen y cómo aparece. Intenta predecir dónde se formará una imagen dada la distancia del objeto y los parámetros ópticos.
Ficha
Optica geométrica II
En esta segunda simulación de la óptica geométrica de las lentes delgadas, se explica cómo se forma una imagen mediante una lente convergente/divergente o un espejo. Determina cómo el cambio de los parámetros de la óptica afecta dónde aparece la imagen y cómo se ve. Intenta predecir dónde se formará una imagen dada la distancia del objeto y los parámetros ópticos.
Ficha
Laboratorio virtual de lentes delgadas
En esta simulación de lentes delgadas se puede estudiar qué ocurre en la imagen formada por una lente al cambiar la distancia focal y la altura y posición del objeto.
Cuando estés listo para empezar, pulsa el botón «Begin».
Espesor y curvatura de una lente delgada
Esta simulación de lentes delgadas permite estudiar cómo cambia el punto focal de una lente al cambiar su espesor y curvatura. Mueve el control y observa los resultados.
Optica geométrica I
En esta primera simulación de la óptica geométrica de las lentes delgadas, se explica cómo se forma una imagen con una lente convergente o un espejo plano. Determina cómo el cambio de los parámetros de una lente afecta el lugar donde se forma la imagen y cómo aparece. Intenta predecir dónde se formará una imagen dada la distancia del objeto y los parámetros ópticos.
Ficha
Optica geométrica II
En esta segunda simulación de la óptica geométrica de las lentes delgadas, se explica cómo se forma una imagen mediante una lente convergente/divergente o un espejo. Determina cómo el cambio de los parámetros de la óptica afecta dónde aparece la imagen y cómo se ve. Intenta predecir dónde se formará una imagen dada la distancia del objeto y los parámetros ópticos.
Ficha
Fundamentos de Electromagnetismo para Ingeniería
Fundamentos de Mecánica para Ingeniería
Herramientas de Teledetección óptica y SAR
Fundamentos de Comunicaciones Ópticas
