Fourier Series. Introduction and applications

What are Fourier series

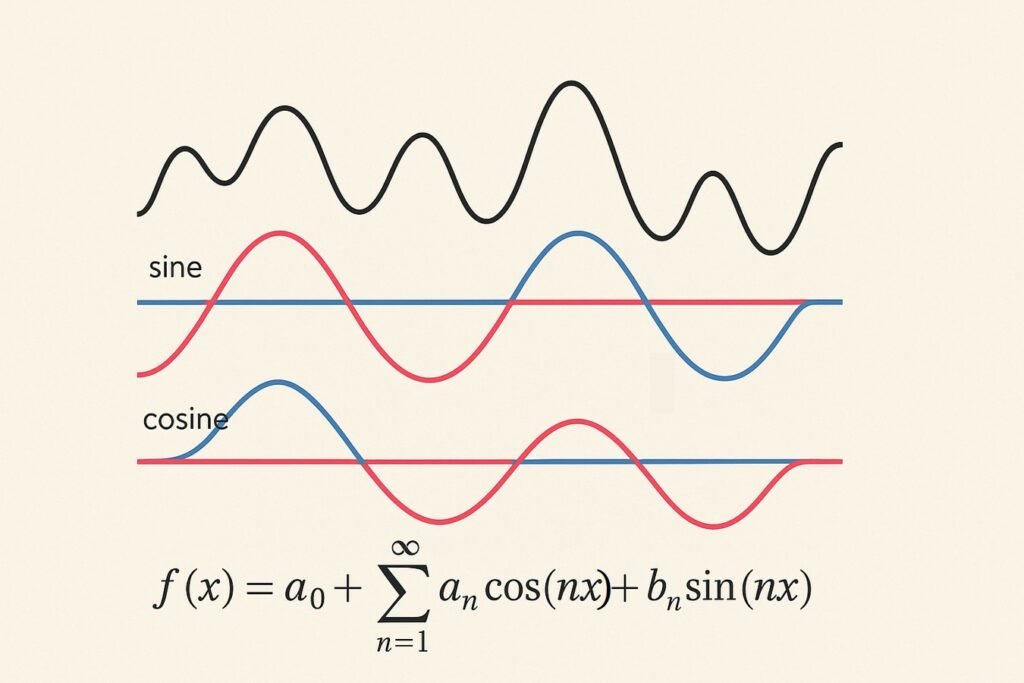
Fourier series is a mathematical technique used to represent periodic functions as an infinite sum of sine and cosine functions. They were developed by the French mathematician Joseph Fourier in the 19th century as a tool for studying heat conduction in solids.

Introduction to Fourier series

The basic idea behind Fourier series is that any periodic function can be decomposed into a series of sinusoids of different frequencies and amplitudes. This means that if we know the frequencies and amplitudes of the sinusoids that make up a periodic function, we can represent that function as a sum of those sinusoids. The representation of a function in terms of Fourier series allows us to analyze its behavior at different frequencies and is used in areas such as engineering, physics and telecommunications.

Approaches in mathematical analysis

The decomposition of a function in terms of Fourier series is performed by calculating integrals. This process allows determining the coefficients that represent the amplitudes of the individual sinusoids that compose the original periodic function. The integrals are calculated over a complete period of the function, which ensures that each frequency component is correctly matched to the waveform.

There are different techniques for performing this decomposition, including the classical Fourier series, which uses trigonometric expressions, the complex Fourier series, which uses complex numbers to simplify calculations, and the trigonometric Fourier series, which focuses on representation by specific sines and cosines. Each method has particular applications depending on the mathematical or physical context in which they are being used, from equation solving to signal synthesis in telecommunications.

Applications of Fourier series

Fourier series have a wide variety of applications in areas such as signal processing, where they are used to analyze and synthesize electrical and acoustic signals, facilitating the elimination of noise and the improvement of transmission quality. They are also fundamental in the resolution of partial differential equations, especially in problems related to heat diffusion and fluid dynamics. In mechanical vibration analysis, Fourier series are used to identify natural frequencies of structures and systems, which is essential in the design and maintenance of machinery and buildings.

In addition, these series play a crucial role in communication theory, allowing the representation of signals in terms of frequencies and assisting in the modulation and demodulation of signals in telecommunications. In electrical engineering, they are used to design and analyze electronic circuits and control systems. In physics, they are key tools for studying periodic phenomena such as electromagnetic waves and atomic vibrations. Finally, in digital image and video processing, Fourier series help to improve image quality and to perform spectral analysis for the detection of specific patterns.