Series de Fourier. Introducción y aplicaciones

Qué son las series de Fourier

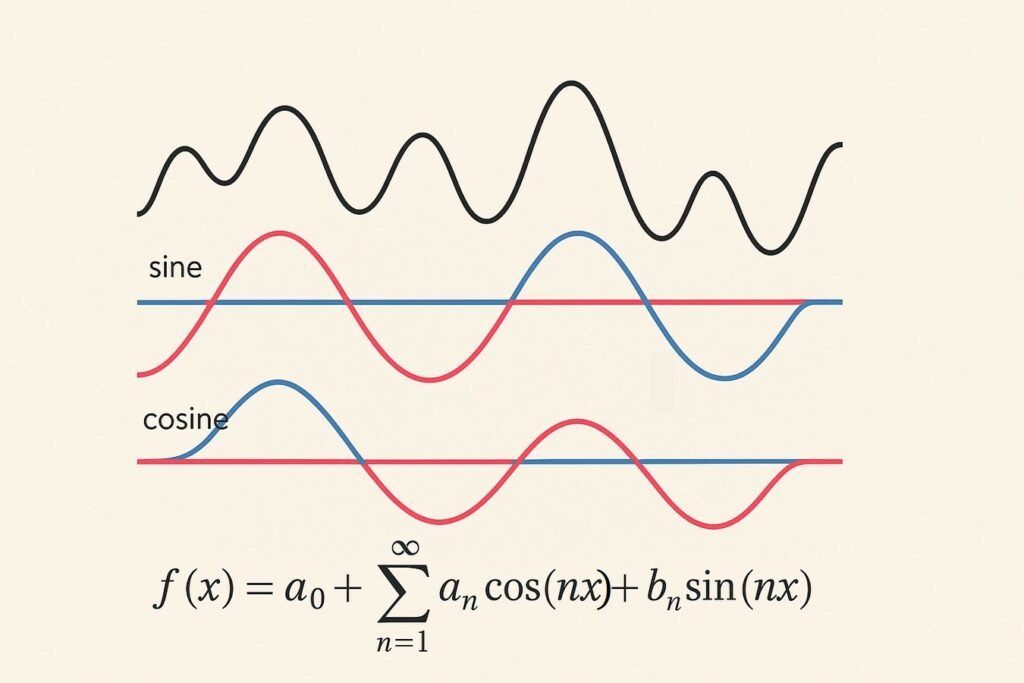
Las series de Fourier son una técnica matemática utilizada para representar funciones periódicas como una suma infinita de funciones senoidales y cosenoidales. Fueron desarrolladas por el matemático francés Joseph Fourier en el siglo XIX como una herramienta para estudiar la conducción del calor en sólidos.

Introducción a las series de Fourier

La idea básica detrás de las series de Fourier es que cualquier función periódica se puede descomponer en una serie de sinusoides de diferentes frecuencias y amplitudes. Esto significa que si conocemos las frecuencias y amplitudes de las sinusoides que componen una función periódica, podemos representar esa función como una suma de esas sinusoides. La representación de una función en términos de series de Fourier permite analizar su comportamiento en diferentes frecuencias y es utilizada en áreas como la ingeniería, la física y las telecomunicaciones.

Enfoques en el análisis matemático

La descomposición de una función en términos de series de Fourier se realiza mediante el cálculo de integrales. Este proceso permite determinar los coeficientes que representan las amplitudes de las sinusoides individuales que componen la función periódica original. Las integrales se calculan a lo largo de un periodo completo de la función, lo que asegura que cada componente frecuencial se ajuste correctamente a la forma de onda.

Existen diferentes técnicas para realizar esta descomposición, entre ellas se encuentra la serie de Fourier clásica, que utiliza expresiones trigonométricas, la serie de Fourier compleja, que emplea números complejos para simplificar los cálculos, y la serie de Fourier trigonométrica, que se centra en la representación mediante senos y cosenos específicos. Cada método tiene aplicaciones particulares dependiendo del contexto matemático o físico en el que se estén utilizando, desde la resolución de ecuaciones hasta la síntesis de señales en telecomunicaciones.

Aplicaciones de las series de Fourier

Las series de Fourier tienen una amplia variedad de aplicaciones en áreas como el procesamiento de señales, donde se emplean para analizar y sintetizar señales eléctricas y acústicas, facilitando la eliminación de ruido y la mejora de la calidad de la transmisión. También son fundamentales en la resolución de ecuaciones diferenciales parciales, especialmente en problemas relacionados con la difusión del calor y la dinámica de fluidos. En el análisis de vibraciones mecánicas, las series de Fourier son utilizadas para identificar frecuencias naturales de estructuras y sistemas, lo que resulta esencial en el diseño y mantenimiento de maquinaria y edificios.

Además, estas series desempeñan un papel crucial en la teoría de la comunicación, permitiendo la representación de señales en términos de frecuencias y ayudando en la modulación y demodulación de señales en telecomunicaciones. En la ingeniería eléctrica, se utilizan para diseñar y analizar circuitos electrónicos y sistemas de control. En la física, son herramientas clave para estudiar fenómenos periódicos como las ondas electromagnéticas y las vibraciones atómicas. Por último, en el procesamiento digital de imágenes y videos, las series de Fourier ayudan a mejorar la calidad de las imágenes y a realizar análisis espectrales para la detección de patrones específicos.